ISO/IEC Guide 98-4的應用
以量測不確定度、符合性聲明與判定規則的連動關係為例
依據本會過往辦理實驗室主管在職訓練與報告簽署人在職訓練,實驗室同仁對於訓練主題的需求調查,量測不確定度一直是大家最關心的主題之一。特別是新版ISO/IEC 17025:2017標準發布後,有關「量測不確定度」、「符合性聲明」、「判定規則」的要求,也是實驗室工作者關心的議題。本篇是入門級文章,希望在不使用任何數學公式的情況下,讓實驗室夥伴們了解量測(Measurement)運用於校正(calibration)與測試(testing)的情境,更進一步理解在ISO/IEC 17025:2017中,量測不確定度、符合性聲明與判定規則的連動關係。本文為筆者個人研究的觀點及分享,未來本會將參考ISO/IEC Guide 98-4與即將公告的新版ILAC G8內容,修訂本會指引文件「測試與校正結果與規格符合性之陳述方法(TAF-CNLA-G04)」,作為申請本會認證的指引性文件。
量測不確定度(Measurement Uncertainty)
量測不確定度的第一個核心概念就是“真值(True Value)不可知,但不會變化;量測值(Measurement result, 又稱量測結果)可知,但會變化”。 對任何一個物理量進行的量測,都不可能得出一個絕對正確的數值,即使運用最先進完善的量測儀器與方法,仍是使用另一個工具來取得相對的量測值,不是絕對值。故量測出的量測值一定會與真值存在差異。所以當假設某個受測(校)件的量測結果(ex: 某個法碼的質量)的真值是“▼”時,在確認過量測過程都是正確的前提下,經過多次(趨近於無限次)的重複量測後,量測結果出現不同數值的機率,會以統計上所稱的機率密度函數(Probability Density Function, PDF)呈現。當量測方法與性能特性有差異時,就會產生不同類型的機率密度函數。可能是對稱、可能是不對稱。一般理想情況下,會是如下的常態分布(Normal Distribution)。但因實務上常無法進行多次量測(樣本數需大於30),實驗室在進行量測不確定度評估時,常會使用T分布(Student's T-distribution)來推估量測結果的實際機率分布情況。
 圖(一): 重複量測的常態分布圖
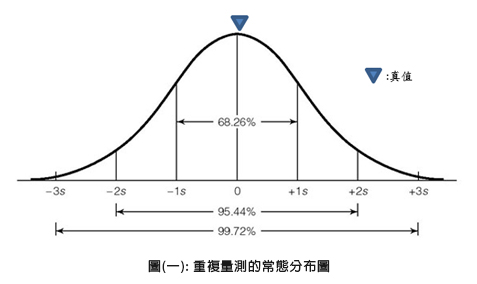
圖(一): 重複量測的常態分布圖
其中s表示該常態分布的標準差。當以文字來描述上述的曲線時,實驗室可以表示其量測結果有68.26 %的機率,落在+s與-s之間。也可以表示其量測結果有99.72 %的機率,落在+3s與-3s之間。為維持在測試報告中提供量測不確定度資訊的一致性,TAF在量測不確定度之政策(TAF-CNLA-R06)中,要求實驗室於報告中呈現量測不確定度之表達應使用y ± U(y和U同單位)表示,並應在證書/報告中註明不確定度的涵蓋因子及涵蓋機率(或信賴水準)。唯要留意的是,報告以使用y ± U作為量測不確定度之表達方式,一般是假設最終得到的擴充不確定度是在各不確定度分量變數組合後,其機率分布特性為對稱分布或近似對稱分布。而實驗室若確認其所評估各不確定度分量變數組合後,機率分布為常態分配的條件下,實驗室可描述其量測結果會有95.44 %的機率,落在+2s與-2s之間,並常會以“本報告的擴充不確定度,係以組合標準不確定度乘以涵蓋因子k=2來表示,相應之信賴水準約為95 %”的文字,來描述其量測不確定度。
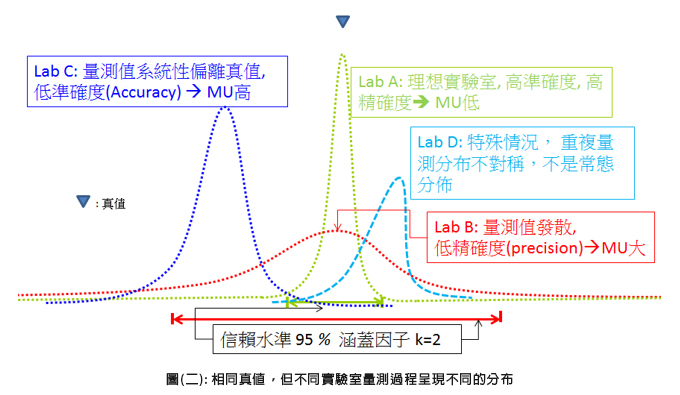
此時可以發現,用量測不確定度來代表不同實驗室間的量測能力,是目前ILAC與BIPM採用的最好方式。參考圖(二)可清楚鑑別不同實驗室,受準確度與精確度的影響,而呈現不同量測不確定的關係。特別要提到的是,不見得重複量測的結果,一定會是以常態分布的形式呈現。如同中的Lab D,某些特殊的量測結果,可能會是以不對稱或是其他類型的分布狀態呈現。此時就需要進一步的補充說明,來呈現實驗室的量測不確定度。
 圖(二): 相同真值,但不同實驗室量測過程呈現不同的分布
圖(二): 相同真值,但不同實驗室量測過程呈現不同的分布
一般來說,Lab B可透過內部的品管活動、如人員訓練、設備升級、實驗室內比對(Intra laboratory Comparisons )等方式,讓實驗室量測能力往 Lab A趨近。但Lab C能力要往Lab A提升,常會需要透過設備送外部校正、或是參加實驗室專業能力試驗(proficiency test)或實驗室間比對(Inter laboratory Comparisons )才能鑑別與發現實驗室的量測結果與真值的偏差。這也是外部品管措施的重要性。
符合性聲明(Statement of Conformity)
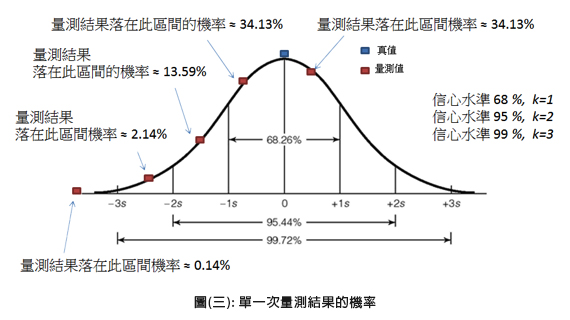
當多次量測的結果,以常態分布的機率形式呈現時,僅依靠單一次或少數次的量測結果,不易鑑別量測值與真值間的差異與相互關係。當量測值與真值間的差異無法100 %確定,卻又必須依據不確定的量測值做出通過/不通過的符合性聲明時,就會產生錯誤符合性聲明的風險性。圖(三)是假設某個重複量測的結果是以常態分布呈現,單一依次量測的結果,落在不同標準差區段的機率。
 圖(三): 單一次量測結果的機率
圖(三): 單一次量測結果的機率
實驗室在陳述某個量測結果,是否符合特定要求(requirements)的行為,即稱為符合性聲明(Statement of Conformity)。在確認某個物件(item)的特性,是否符合某個特定要求時,一般會有上限、下限或是某個特定要求區間等三種情況。在ISO/IEC Guide 98-4中,將上限與下限統稱為允收限制值(Tolerance limit)。上下兩個允收限制值,則形成一個允收區間(Tolerance interval)。故允收區間與允收限制值之觀念差異不大,主要是封閉型要求或是開放型要求的差異。
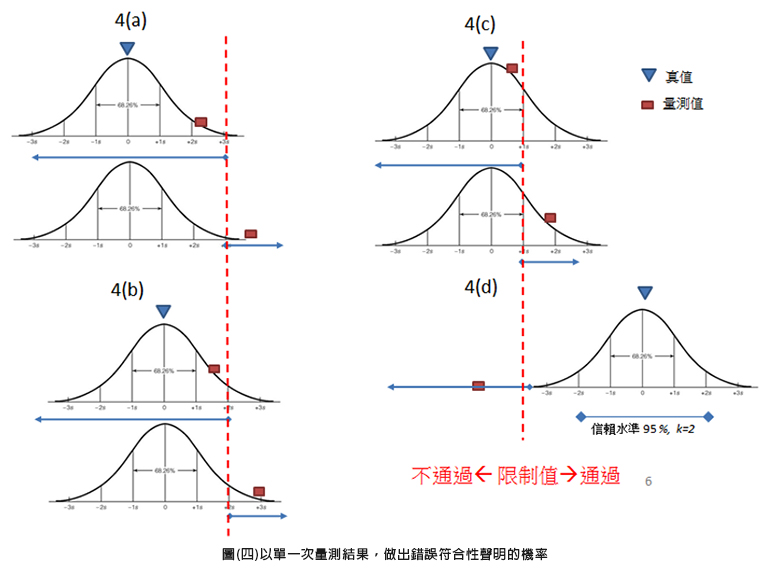
理論上當實驗室進行多次量測後(趨近於無限次),可以得到如圖(三)的常態分布曲線,也可得知真值的合理值範圍。但實務上,實驗室不可能有進行多次數量測的機會。多是依賴單一次的量測結果,來進行符合性聲明。當真值越靠近限制值時,僅依靠一次量測結果,就逕行做出通過/不通過的符合性聲明時,就會有越高的錯誤符合性聲明的機率。這個可能發生的錯誤符合性聲明的情境與機率,就是ISO/IEC Guide 98-4中所提的第一個重要觀念。圖(四)就是描述當真值距離限制值不同位置時,可能做出錯誤符合性聲明的機率:
 圖(四)以單一次量測結果,做出錯誤符合性聲明的機率
圖(四)以單一次量測結果,做出錯誤符合性聲明的機率
在圖4(a)的情境,真值小於限制值3倍標準差(3s),正確的符合性聲明是不通過。當只進行一次量測,量測值落在+3s以下的機率是99.86 %,故有99.86 %的機率會做出正確的符合性聲明(真值小於限制值、也依量測值小於限制值而正確地判定為不通過)。當然,量測值仍有0.14 %的機率會落在+3s以上,故仍有0.14 %的機率做出錯誤的符合性聲明(真值小於限制值、卻因量測值大於限制值而錯誤地判定為通過)。
在圖4(b)的情境,真值小於限制值2倍標準差(2s)時,只進行一次量測,量測值落在+2s以下的機率是97.72 %,故有97.72 %的機率會做出正確符合性聲明,2.28 %的機率做出錯誤符合性聲明。當真值再往限制值靠近,如圖4(c)接近到小於一個標準差(s)時,只進行一次量測,量測值落在+s以下的機率是84.13 %,故有84.13 %的機率會做出正確符合性聲明,15.87 %的機率做出錯誤符合性聲明。有此可看出,當真值越接近限制值,做出錯誤符合性聲明的機率越接近50%。
當真值遠大於限制值時,如圖4(d)時,只進行一次量測,量測值落在限制值以上的機率接近100 % (但不是100 %),落在限制值以下的機率接近0 % (但仍不是0%),故仍有趨近於0 %的機率做出錯誤的符合性聲明。
這是用樣本資料來估算,表示指定比例的總體上下限的機率。既然依統計理論,學理上無論量測值距離限制值有多遠,都不能排除做出錯誤符合性聲明的可能性,實務上實驗室就必須有一套機制,來描述其判定通過/不通過的依據。這套機制,就是判定規則。這也是ISO CASCO在制訂ISO/IEC 17025:2017等運用到量測結果做符合性聲明符合性的標準時,特別強調並加入的概念。
判定規則(Decision Rule)
真值不可得,實驗室只能靠大量的量測才能推估真值所在範圍。但實務上實驗室無法每次量測時,都進行大數量的重複量測來確認真值的範圍,只能依靠一次或是少次數的量測結果,就做出符合性聲明。此時就會有一定機率,做出錯誤的判斷。為了清楚呈現量測不確定度所造成的錯誤符合性聲明的風險與可能會發生的機率,實驗室的判定規則須清楚描述量測值、量測不確定度與符合性限制值之間的關係,並據此作出通過/不通過的符合性聲明,取得客戶同意。
在ISO/IEC 17025: 2017第7.8.6.2節,提及在陳述符合性聲明時,可參考ISO/IEC Guide 98-4。這份文件主要提供了,當要確認某個物件(item)是否符合某個特定要求時的指引與做法。ISO/IEC Guide 98-4除了定義前一章節中提到的允收區間/限制,來表示特定要求,另一個重要觀念就是定義接受區間/限制(Acceptance interval/limit)區間的概念。
實務上在制定判定規則時,會以量測值與量測不確定的關係,來描述實驗室的判定規則。ISO/IEC Guide 98-4中舉例了幾種接受區間的類型與判定規則,主要分為簡單接受與保護帶判定規則兩種主要類型:
簡單接受(Simple acceptance)判定規則
簡單接受有時也稱為“風險分攤”,此判定規則的概念,就是當量測值落在允收區間之間,即視為符合(反之視為不符合)。並將可能作出錯誤符合性聲明的風險明白告知,由顧客與實驗室雙方共同承擔。一般為了在承擔風險這議題上取得雙方共識,會將量測不確定度(雙方合意接受)納入考量。
舉一個運用量測不確定度的簡單接受的範例。假設實驗室要執行量測並確認量測值必須落在D+與D-之間(允收區間是D),方得視為符合。實驗室執行這個量測的擴充不確定度是d(涵蓋因子k=2),如圖(五)所示。
 圖(五)簡單接受判定規則的範例
圖(五)簡單接受判定規則的範例
經與客戶溝通後,實驗室與顧客合意的判定規則如下:
- 量測值必須要在D+與D-之間才能判斷為符合。
- 量測行為的擴充不確定度,必須小於允收區間的三分之一。(d < D/3)
這個判定規則的核心觀念,就是實驗室的量測能力要夠好夠準(以量測不確定度來鑑別),量測的結果就可受信賴。但至於要多準,本範例是舉1/3的允收區間為例。實務上在考量風險後,可能會選擇更嚴格的(如1/10)的允收區間或更寬鬆。選擇嚴格與寬鬆之間的風險,應由實驗室與顧客雙方合意接受。
另一個實務上常見到的簡單判定規則,是在ISO/IEC Guide 115中提到的準確方法(Accuracy method)判定規則。這個判定規則的概念,就是要求實驗室透過下列方式來掌握量測的變異來源,以降低量測不確定度。
- 確認使用的量測儀器的誤差(error)夠小(低於特定要求值)
- 環境影響的影響夠小(低於特定要求值)
- 實驗室的量測程序,有足夠地文件化
- 實驗室人員的量測能力,有足夠地文件化
當這些變異來源都能清楚地掌握時,實驗室在估算(estimate)量測值並判定通過/不通過時,可假設量測不確定度的影響是可忽略並不需評估(evaluate)。這個IEC guide 115的準確方法判定規則,對使用最新科技的量測儀器來執行成熟穩定的測試方法時,對電性領域實驗室提供的一個務實並可操作的判定規則。
總結來說,簡單接受判定規則的類型有很多種,實驗室須依風險程度,在嚴格與寬鬆之間,選擇適當的判定規則並與顧客取得共識。最終,由雙方共同承擔可能做出錯誤判定的風險。
保護帶(Guard bands)判定規則
保護帶判定規則有時也稱為 “嚴格(stringent)接受”判定規則,是簡單接受判定規則的延伸。當量測值接近允收限制時,會因為量測不確定度以機率密度函數呈現的特性,提高了做出錯誤判定的機率。保護帶判定規則的概念,即是在允收限制或允收區間之前加上一個保護帶,以降低做出錯誤判定的機率。這時就要介紹ISO/IEC Guide 98-4中的另一個概念: 接受限制值(Acceptance limit)。如於前面符合性聲明章節所述,某個量測值是否符合允收限制值,會受到量測不確定度的影響。透過實驗室與顧客另定義一個雙方合意的較嚴格的接受限制值,僅當量測值符合接受限制值時,實驗室才判定為符合(反之判定為不符合)。此作法是稱為保護接受(Guided acceptance) 判定規則。同樣地,上限與下限兩個開放式的接受限制值,會形成一個封閉式的接受區間(Acceptance interval)。接受限制與允收限制之間的差值,即是保護帶。
圖(六)是以一個符合上限要求的案例,描述接受限制、允收限制與保護帶的關係。實驗室與顧客合意採用較嚴格的標準,當量測結果落在保護帶時判定為不符合。為了降低作出錯誤的符合聲明(依據允收限制),在情景(a)與(b)才判定為符合,情境(c)~(g)則判定為不符合。可以留意到在情境(b)與(c),即使因接近邊界造成做出錯誤符合性聲明的機會很高,最終仍是依量測值落是在保護帶還是低於接收限制,來判斷是否通過,忽略掉量測不確定度的影響。這是因為情境(b)與(c)量測結果,已遠離允受限制值,真值會在允收限制以上的機率是很低的。情境(f)會有很高的機率,真值是低於允收限制而造成錯誤符合性聲明。但本案例為降低風險,仍是將其視為不通過。
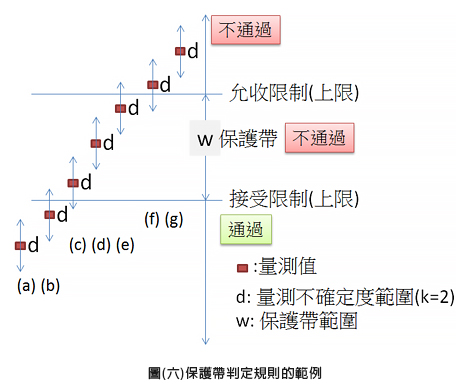 圖(六)保護帶判定規則的範例
圖(六)保護帶判定規則的範例
以EMC測試的輻射干擾量測為例,美國FCC不希望電子設備產生過強的電磁波干擾其他電機電子設備,故規定960 MHz以上的3 m電場強度平均值的最大限制值是54 dBuV/m。實驗室為了降低錯誤報告的風險,故設定保護帶為6 dB,量測值要低於48 dBuV/m才視為為符合。但客戶可能會認為這6 dB保護帶過於嚴格,造成過多合格品被誤判為不符合,故要求保護帶改為3 dB。
此時就產生一個議題,圖(六)中保護帶範圍w要設為多少才合理? 這時除了風險與技術議題,多會將量測不確定度的機率特性納入考量。以一個量測不確定度範圍(k=2)為d實驗室來說,其量測結果約會有95 %的機率落在d的範圍之內。一般常見的作法,是將保護帶範圍設為與量測不確定度相同(d=w)。當然實驗室與顧客,可能因為風險等級來提高或是縮小保護帶。
與保護接受相反,有時接受限制值會比允收限制更寬鬆,這時量測值可能會超過允收限制,但實驗室仍判定為符合。此作法稱為保護拒絕(Guided rejection)判定規則。是否開立高速公路的超速罰單的判定規則,就是一個典型的保護拒絕。當高速公路的速限是100 km/h時,依法超出速限就是違規。但因為開立罰單可能會涉及後續的法院訴訟問題,警察要有提高確定違規的信心,故只有當測速器量到超過110 km/h時,才會開立罰單。此時,速限100 km/h就是允收限制值,110 km/h就是接受限制值,10 km/h就是保護帶。
結語
在測試與校正領域中,有各種不同類型的符合性聲明的情境,實驗室也會定義千百種各種不同類型的判定規則。雖然這些眾多的做法,可以回歸到簡單接受與保護帶判定規則這兩類,但期望一套做法就能適用於所有情境,無異緣木求魚。標準與文件中的範例與情境並不是唯一作法。實驗室應該依本身產業特性與風險程度制定合適的判定規則。
風險分攤是符合性聲明與判定規則的核心觀念。量測不確定度則是量化風險的重要工具。因此無論是哪一種類型的判定規則,都要明白告知客戶可能會發生錯誤判定的機率與風險,並在取得雙方合意後執行。這也是為何在ISO/IEC 17025: 2017中,新增判定規則的定義、新增於合約審查時就要取得客戶同意判定規則的要求(第7.1.3節)、並在結果的報告中,要求清楚地識別所使用的判定規則(第7.8.6.2(c)節)。
希望透過這篇入門文章,讓檢測驗證產業的從業人員了解量測不確定度、符合性聲明與判定規則的連動性與其背後的物理意義。對簡單接受、準確方法、保護接受與保護拒絕等判定規則也有正確的理解。幾個專有名詞的詳細說明與其應用,限於篇幅無法詳述。若希望進一步了解細節,可以自行研讀相關規範或與筆者聯繫了解。
再次聲明,本文為筆者個人研究的觀點及分享,未來修訂的「測試與校正結果與規格符合性之陳述方法(TAF-CNLA-G04)」,才是作為協助實驗室了解認證要求的正式指引性文件。若對將修訂中的新版TAF-CNLA-G04內容有任何指導與建議,歡迎與筆者聯繫。
另涉及在特定領域中,如何運用量測不確定度制定合適的判定規則,請與本會相關領域的同仁聯絡。本會同仁另針對校正領域的幾種實際的判定規則,有舉出更多完整的實例,可參考相關連結。


